بررسی پیاده‌سازی‌های مختلف حلقه در سی‌پلاس‌پلاس

به نام خدا

معرفی

این پست، بیشتر یک پست معرفی است. امروز یک وبلاگ جدید پیدا کردم که نویسنده‌ی آن تصمیم دارد به مباحثی در برنامه‌نویسی با تمرکز بر روی زبان C++ بپردازد. وبلاگی که معرفی شد Random Programming نام دارد.

پیشنهاد پست

فعلاً تعداد پست‌های این وبلاگ به خاطر اینکه تازه تاسیس شده است زیاد نیست. ولی در میان پست‌های وبلاگ، یک سری از پست در مورد انواع پیاده‌سازی حلقه در حالات مختلف در C++ می‌باشد. خواندن این پست‌ها را بسیار توصیه می‌کنم. بخصوص قسمت‌هایی از پست‌ها به پیاده‌سازی با استفاده از امکانات STL در C++11 پرداخته است.

1. در پست اول این سری، صورت مسئله این است. یک محموعه از اشیا داریم، چگونه می‌توانیم بر روی همه‌ی اشیاء این محموعه تابعی را اجرا نماییم؟ راه‌کارهایی که معرفی شده‌اند در ادامه توسط نویسنده کاملاً بررسی شده و مزایا و معایب هر کدام گفته شده است. این پست را می‌توانید در این آدرس مشاهده کنید.

2. در این پست، مسئله مشابه پست قبلی است. فرق در این است که در اینجا علاوه بر اشیا مجموعه به تابع آرگومان دیگری نیز پاس داده می‌شود. این پست را نیز می‌توانید در این آدرس مشاهده کنید.

3. در پست سوم این مسئله بررسی شده است که چگونه می‌توان تابع عضو (member function) را بر روی اعضای یک کلاس درون یک مجموعه صدا زد؟ این پست نیز در این آدرس قرار دارد.

4. مسئله چهارم به این شکل است. فرض کنید مجموعه‌ای از اشیا از یک کلاس داریم. می‌خواهیم از روی هر یک از اشیاءِ این محموعه، اشیائی از یک کلاس دیگر بسازیم و در مجموعه‌ای دیگر قرار دهیم. این کار را چگونه می‌توان انجام داد؟ راه‌حل‌های پیشنهادی برای این مسئله نیز در این پست آمده است.

کامپایلر مایکروسافت برای پایتون

به نام خدا

مقدمه

اخیراً شروع به کار با زبان پایتون کردم. خیلی سبک زبان رو نپسندیدم، بخصوص با dynamic بودن هنوز کامل کنار نیامده‌ام. ولی زبان پایتون جامعه‌ی بسیار بزرگی دارد و نتیجه‌ی این جامعه‌ی بزرگ پروژه‌های باکیفیت و پرتعداد و پرکاربردی است که برای این زبان و با این زبان ایجاد شده‌اند. همین کتابخانه‌ها برنامه‌نویسی را برای انجام بسیاری از کارها آسان می‌کند.

برای نصب کتابخانه‌های مختلف برای این زبان، راه‌های مختلفی وجود دارد. مشهورترین این راه‌ها pip و easy_install است. همچنین با استفاده از conda نیز می‌توان این کار را برای بعضی از کتابخانه‌ها انجام داد.

ولی راه اصلی نصب بسیاری از کتابخانه‌ها، استفاده از دستور زیر است:

>> python setup.py install

فایل setup.py در همه‌ی پروژه‌ها وجود دارد، و در واقع این فایل توسط توسعه‌دهندگان هر کدام از این کتابخانه‌ها نوشته می‌شود. با استفاده از این دستور می‌توان کتابخانه‌ی مورد نظر را به لیست پایتون اضافه کرد.

پایتون به زبان C نوشته شده است و برای سرعت‌گرفتن، قسمت‌هایی از کد را می‌توان به زبان C نوشت و در کد پایتون استفاده کرد. همچنین پروژه‌ای همانند Cython می‌تواند کد پایتون را به کد C تبدیل کند.

مشکل

در هنگام نصب بعضی از پروژه‌ها، لازم است قسمتی از کد توسط یک کامپایلر C کامپایل شود. برای این کار باید پایتون بتواند کامپایلر درست نصب شده و تنظیمات مناسب را تشخیص دهد. اگر این مشکلی در این کار پیش بیاید، خطایی مانند زیر در هنگام نصب کتابخانه نمایش داده خواهد شد:

Error:unable to find vcvarsall.bat

این خطا بخصوص در ویندوز احتمال ظهور بیشتری دارد! برای اینکار راه‌حلی پیشنهاد می‌شود که در ادامه توضیح آن را خواهم داد.

راه‌حل

در مسیر زیر فایلی به نام distutils.cfg وجود دارد

%PYTHONDIR%\Lib\distutils\

اگر هم این فایل موجود نباشد، آن را ایجاد کنید. محتویات آن را به صورت زیر تغییر دهید:

[build]
compiler=msvc

%PYTHONDIR% مسیر نصب پایتون می‌باشد. مسیر پیش‌فرض مسیر زیر می‌باشد:

C:\Python27

تنظیمات بالا با فرض این است که کامپایلر مایکروسافت بر روی سیستم نصب باشد. اگر ویژوال استودیو داشته باشید کامپایلر نصب می‌باشد. اگر کامپایلر ویژوال استودیو ندارید می‌توانید نسخه‌ی Express ویژوال استودیو را دریافت و نصب کنید.

حال به مسیر زیر بروید:

%PYTHONDIR%\PCbuild\

در این پوشه فایل زیر را ایجاد کنید

msvcr<num>.def

که منظور از <num> یک شماره است که بر اساس نسخه‌ی ویژوال استودیو تعیین می‌شود

• Visual Studio 2008 -> 90
• Visual Studio 2010 -> 100
• Visual Studio 2012 -> 110
• Visual Studio 2013 -> 120

حال در فایل ایجاد شده دو خط زیر را بنویسید:

LIBRARY MSVCR<num>.dll
EXPORTS

با انجام این کارها به احتمال زیادی مشکل کامپایل‌شدن کدهای C برای پایتون حل خواهد شد.

Spectrogram

به نام خدا

Exponential Chirp Spectrogram

(Creative Commons Attribution-Share Alike 3.0 Unported license (CC BY-SA 3.0), from Wikimedia Commons)

معرفی

برای بررسی ساختار فرکانسی سیگنال‌های متغییر در زمان، از روشی به نام تبدیل فوریه‌ی کوتاه-زمان (STFT) استفاده می‌شود. با استفاده از این نوع تبدیل فوریه می‌توان به اطلاعات فرکانسی و فازی ناحیه‌ای کوتاه از سیگنال پی برد. در حالت پیوسته، این تبدیل از رابطه‌ی زیر به دست می‌آید:

$$ \text{STFT} ‎\lbrace x(t) ‎\rbrace (\tau ,\omega ) \equiv X ( \tau ,\omega ) = \int _{-\infty }^{\infty} x(t)w(t-\tau )e^{-j \omega t}dt $$

که تابع \( w(t)\) تابع پنجره می‌باشد.

رابطه‌ی تبدیل فوریه‌ی کوتاه-زمان برای حالت گسسته نیز مشابه می‌باشد.

$$ \text{STFT} \lbrace x[n] \rbrace (m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty } x[n]w[n-m]e^{-j \omega n} $$

برای تهیه‌ی اسپکتروگرام، سیگنال به بازه‌هایی با طول کمتر از طول سیگنال تقسیم می‌شود (لزومی ندارد این بازه‌ها مجزا باشند)، برای هر کدام از این بازه‌ها تبدیل فوریه محاسبه می‌شود، و سپس اندازه‌ی این تبدیل فوریه برای بازه‌های مختلف در کنار یکدیگر قرار می‌گیرد تا تصویری دو یا سه بعدی از اسپکتروگرام سیگنال اصلی ایجاد شود.

پیاده‌سازی

(نمونه کدها، به زبان متلب می‌باشند)

برای ایجاد نمودار اسپکتروگرام برای یک سیگنال، ابتدا لازم است سیگنال را به تعدادی بازه تقسیم کرده و سپس برای هر بازه، ضرایب فوریه را محاسبه نماییم. در نهایت با جمع‌آوری همه‌ی این ضرایب به دست‌آمده، می‌توانیم نمودار آبشاری اسپکتروگرام را رسم کنیم.

کد زیر یک پیاده‌سازی ابتدایی برای این کار است:

function specPlot(x, windlen)
% x: input signal
% windlen: length of the time window inside which fourier coefficients will be calculated, note that since our signal is real, only half of the coefficients are needed

% preallocating magnitude matrix for speedup
numofwinds = floor(length(x)/windlen);
magnitude = zeros(numofwinds, floor(windlen/2));
for i = 0:(numofwinds - 1)
       startIdx = i*windlen;
       partfft = abs(fft(x((1+startIdx):(startIdx+windlen))))/windlen;
       magnitude((i+1),:) = partfft(1:length(partfft)/2);
end
waterfall(1:windlen/2, 0:(length(x)/windlen -1), magnitude);
xlabel('frequency');
ylabel('time');
zlabel('magnitude');
end

حال این توابع را بر روی یک سیگنال نمونه امتحان می‌کنیم.

سیگنال زیر را که یک سیگنال جیر با رابطه‌ی \( y=sin(1600\pi t^2) \) می‌باشد در نظر بگیرید. نمودار این سیگنال به صورت زیر است:

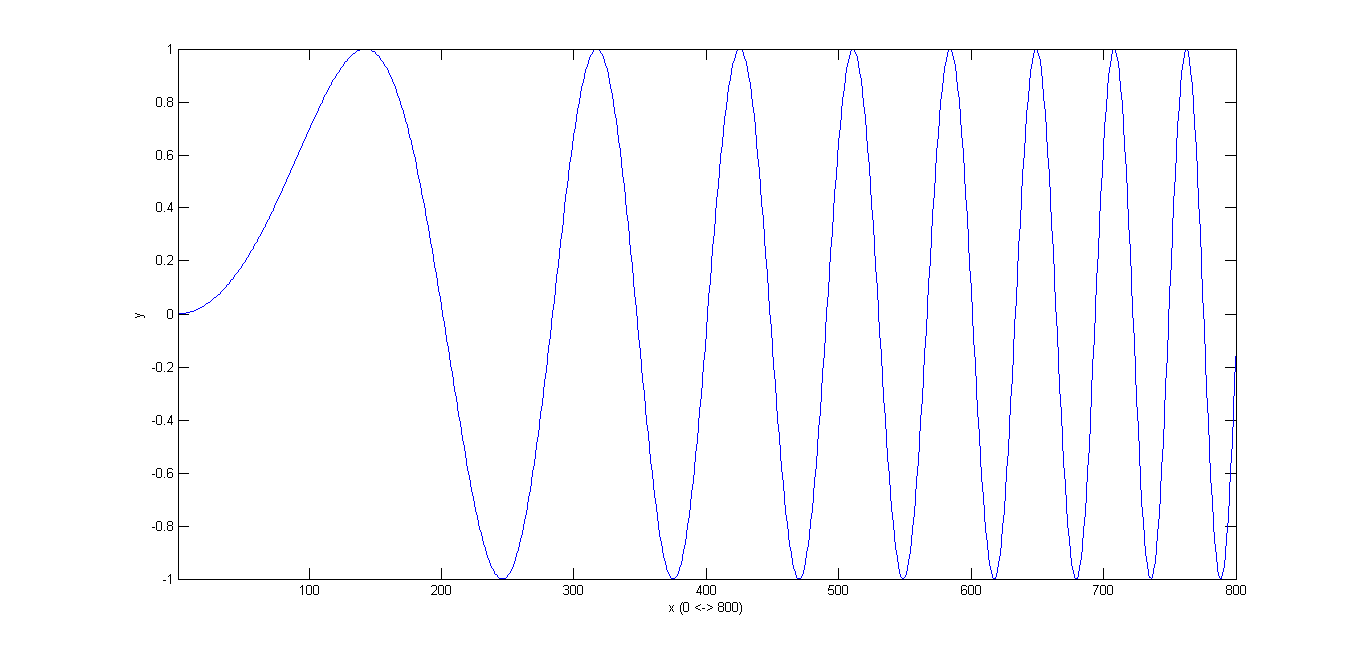
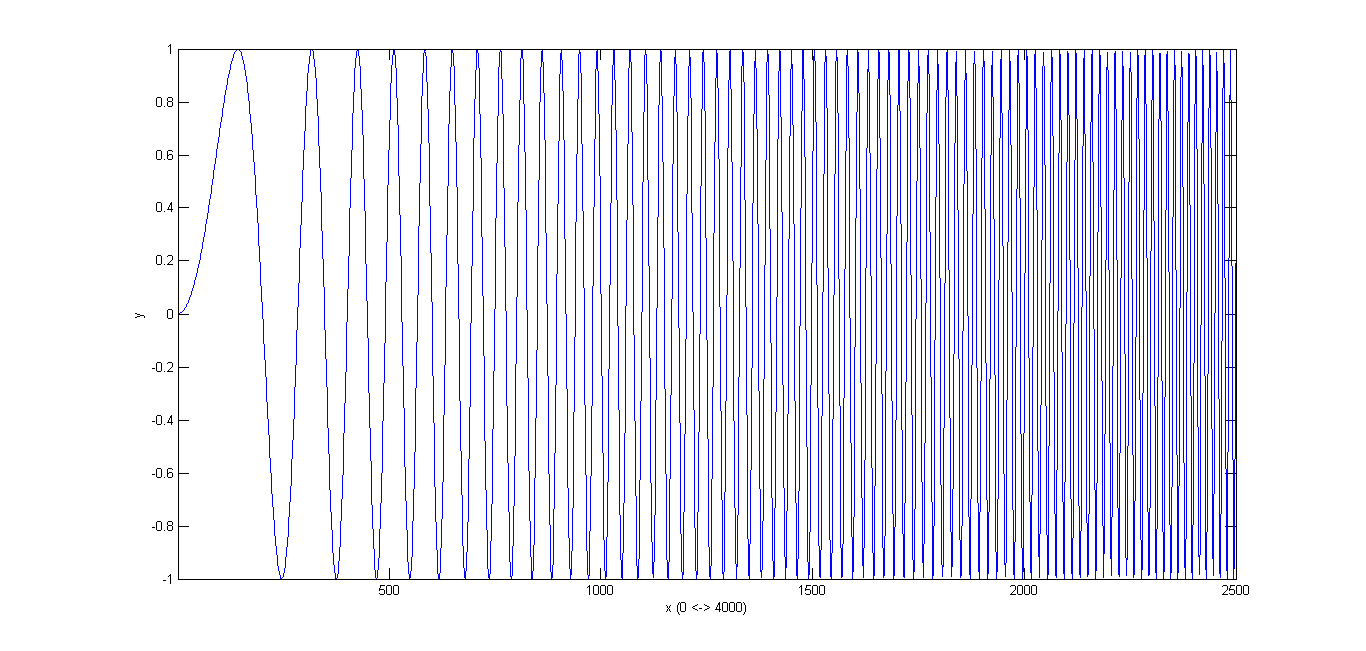
>> t = [0:1/8000:1-1/8000];
>> y = sin(2*pi*800*(t.*t));
>> specPlot(y,800);

با اجرای دستور آخر نمودار زیر ایجاد خواهد شد

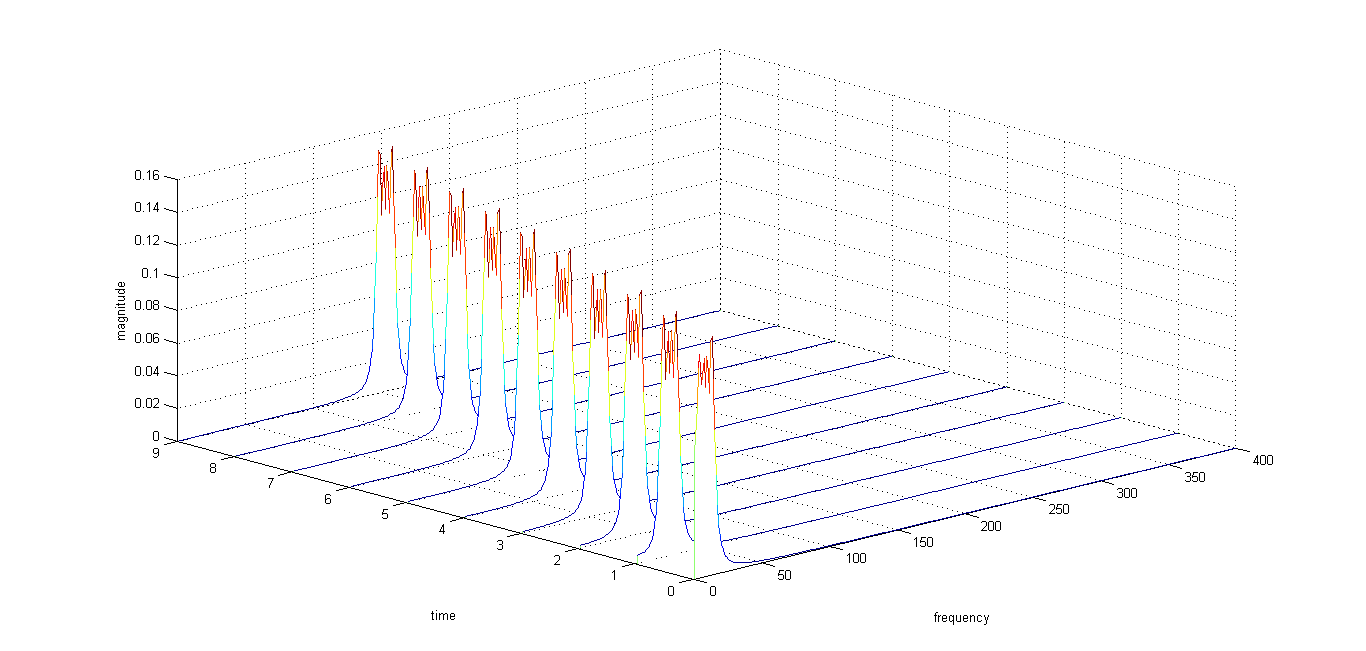
این در مقابل اون

به نام خدا

فرض کنید یک انسان 80 سال عمر بکنه. هر سال را هم به طور متوسط 365.25 روز می‌گیریم، هر روز هم 24 ساعت، هر ساعت 60 دقیقه و هر دقیقه هم 60 ثانیه است.

انسان به طور معمول در هر ثانیه 20 تصویر را می‌بینه، ولی هنگامی که هیحان بالایی داره، این عدد ممکنه تا 60 افزایش پیدا بکنه. حالا ما فرض می‌کنیم که این فرد به طور متوسط در طول عمرش 30 تصویر در ثانیه دیده، هیچ‌وقت هم چشمانش رو نبسته.

با این اعداد، تعداد تصاویری که این فرد در طول عمرش خواهد دید برابر خواهد بود با: $$ 7.5738 \times 10^{10} $$

حالا یک تصویر دیجیتال غیررنگی با سایز 512 در 512 را در نظر بگیرید. هر پیکسل از این تصویر مقداری بین 0 تا 255 به خودش می‌گیره. پس تعداد کل تصاویر ممکن برابر خواهد بود با عدد: $$ 4.5443 \times 10^{631305} $$

مقایسه‌ی جالبی هست به نظرم. توی این همه تصویر، تصویر صورت همه‌ی ما از همه جهات، تصویر صورت همه‌ی دوستانمون، تصویر خودروی آینده‌مون، تصویر فرزندانمون و خیلی تصاویر دیگه هست. ولی ما خیلی راحت، بدون دیدن این همه تصویر، می‌تونیم بفهمیم که توی تصویری صورت هست یا نه.

Pathfinding.js, معرفی و نمایش

به نام خدا

امروز در حین گشت‌و‌گذار میان صفحات با آدرس *.github.io به صفحات جالبی برخوردم. یکی از صفحات مربوط به نمایش امکانات یک کتابخانه‌ی محاسبه‌ی مسیر به زبان جاوااسکریپت بود. کتابخانه اینطوری توصیف شده:

A comprehensive path-finding library for grid based games

اینجا می‌توانید به کد کتابخانه دسترسی داشته باشید.

ولی نکته‌ی اصلی که توجهم را جلب کرد، نمایش قابلیت‌های این کتابخانه در این سایت بود. در این سایت به خوبی نمایشی از نحوه‌ی الگوریتم‌های پیاده‌سازی‌شده در این کتابخانه وجود دارد. حتماً این صفحه را بازدید کنید.

الگوریتم‌های مسیریابی پیاده‌سازی شده در این کتابخانه:

1. A*
2. IDA*
3. Breadth-First-Search
4. Best-First-Search
5. Dijkstra
6. Jump Point Search

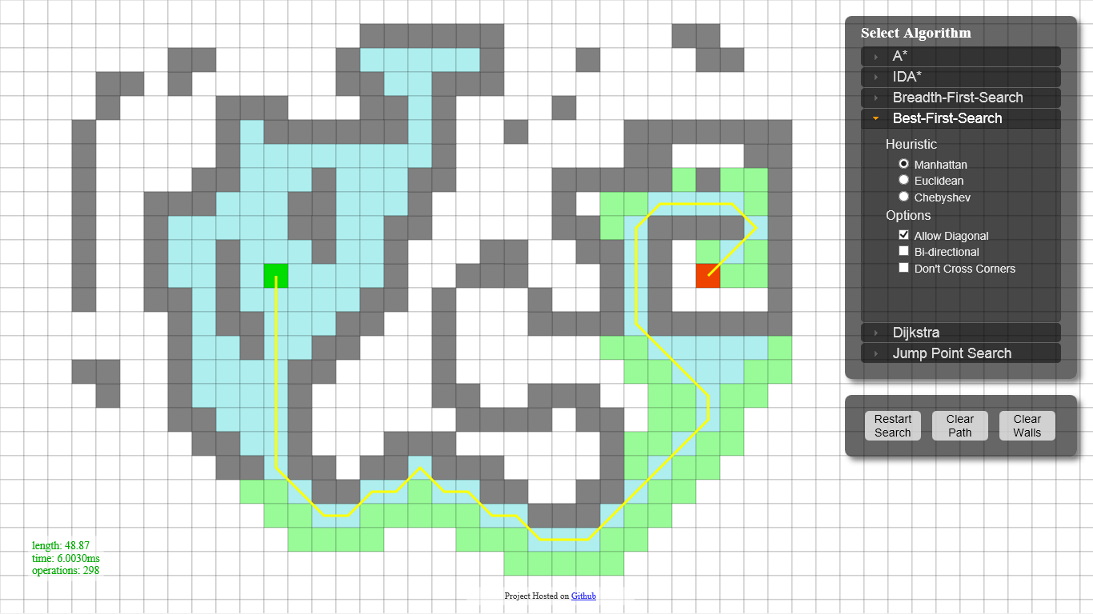
چگونه یک صفحه‌ی گیت‌هاب با استفاده از Sandra.Snow بسازیم؟

به نام خدا

آماده‌سازی اولیه‌ی بلاگ

در این پست می‌خواهم در مورد نحوه‌ی ساخت یک صفحه‌ی گیت‌هاب (Github Pages) با استفاده از Sandra.Snow بنویسم. همین وبلاگی که الان مشاهده می‌کنید با استفاده از این سیستم ساخته شده. چنین سایت‌هایی به صفحات ایستا (Static Webpages) مشهور هستند. در این نوع سایت‌ها، بجز نمایش صفحات، از سمت سرور هیچ عمل خاصی انجام نمی‌گیرد. به همین دلیل هم میزبانی این نوع صفحات بسیار آسان است و به راحتی می‌توان محتوای خوبی با استفاده از این نوع صفحات ایجاد کرد. البته همین ایستا بودن صفحات باعث ایجاد محدودیت‌هایی هم می‌شود ولی می‌توان بعضی از این محدودیت‌ها را با استفاده از امکانات سمت کاربر (Client-side) برطرف کرد. یک نمونه از این امکانات، نظرگذاری در پست‌ها می‌باشد. یکی از راه‌های پیاده‌سازی نظرگذاری در بسیاری از سایت‌ها، ایجاد یک پایگاه‌داده در سمت سرور و مدیریت این نظرات توسط سرور می‌باشد. راه‌حلی که برای سایت‌های ایستا ایجاد شده است، استفاده از سرویس‌هایی همچون Disqus می‌باشد. سرویس‌هایی اینچنین امکان نظر گذاشتن بر روی صفحات ایستا را فراهم می‌سازند. برای فعال‌سازی این نوع نظرات فقط کافی است یک حساب کاربری در این سایت ایجاد نمایید و شناسه‌ی سایت خود را دریافت کنید. با قراردادن این شناسه در فایل تنظیمات، این امکان در صفحات ایستا ایجاد می‌شود. امکانات دیگری نیز وجود دارد که تقریباً همه‌ی آنها وابسته به جاوااسکریپت بوده و سمت کاربر هستند. پس به راحتی می‌توان با پیدا کردن کتابخانه‌های جاوااسکریپت، امکانات بیشتری را به صفحات ایستا افزود. البته باید مسئله‌ی حجم صفحات را نیز در نظر گرفت و از سنگین کردن بیش از حد این صفحات جلوگیری کرد. مثلاً یکی از کتابخانه‌های جاوااسکریپت که در این بلاگ استفاده شده، کتابخانه‌ی MathJax برای نمایش فرمول‌های ریاضی هست. حالا اگر بخواییم خلاصه‌ای از مراحل ایجاد این بلاگ را بگیم به این صورت خواهد بود: اول لازمه که پروژه‌ی زیر رو از گیت‌هاب بر روی کامپیوتر خودتون clone کنید:

git clone https://github.com/Sandra/Sandra.Snow.git

مرحله‌ی بعد این هست که فایل پروژه‌ با نام Sandra.Snow.sln که در پوشه‌ی src قرار دارد را باز کنید. برای اینکار بر روی ویندوز به نرم‌افزار ویژوال‌استودیو نیاز دارید. البته بر روی همه‌ی سیستم‌های عامل می‌توانید از Xamarin Studio استفاده کنید. در اینجا برای ساخت بلاگ، فقط به پروژه‌ای با نام Snow نیاز داریم. در تنظیمات این پروژه، در قسمت debug در قسمت مربوط به Command line arguments اطلاعات زیر رو وارد کنید:

config="path/to/Snow/" server=true debug=true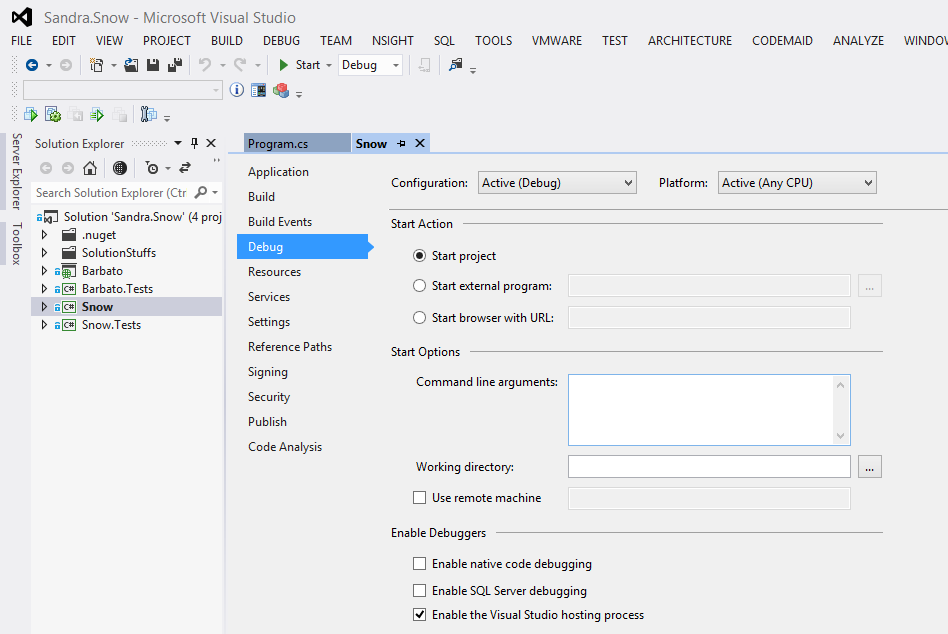

path/to/Snow/ آدرس پوشه‌ی Snow هست که فایل‌های سایت در اون قرار داره. در این پوشه فایل‌های مربوط به تنظیمات صفحات، تنظیمات ظاهر صفحه و همچنین فایل‌های جاوااسکریپت و CSS و عکس‌ها قرار دارند. برای یک نمونه از این نوع پوشه که برای شروع کار آماده است می‌توانید از نمونه‌ای که در این آدرس قرار دارد استفاده کنید. همچنین نمونه‌ی تغییر یافته برای بلاگ‌های فارسی در این آدرس قرار دارد. شما فقط به پوشه‌ی Snow این فایل‌ها نیاز دارید. در نهایت فقط کافی است تنظیمات مربوط به فایل snow.config و در صورت نیاز، فایل‌های *.cshtml موجود در پوشه‌ی themes/snowbytepersian و themes/snowbytepersian/_layouts را تغییر دهید. در این میان مهم‌ترین فایل، فایل default.cshtml می‌باشد. با تغییر این فایل، بسیاری از تنظیمات شما برقرار می‌شوند. در فایل‌های موجود در تِمِ snowbytepersian تنظیمات مربوط به جهت درست نمایش متون و همچنین نمایش فرمول‌های ریاضی درج شده‌اند. با بررسی فایل‌های ذکر شده می‌توانید تنظیمات دلخواه خود را اعمال کنید.

در نهایت بعد از کامپایل کردن پروژه‌ی ذکر شده در ابتدای پست، در صورتی که آدرس پوشه‌ی Snow را به درستی داده باشید، سایت شما ایجاد شده و یک سرور برای نمایش محلی شما ایجاد می‌شود. بعد از اینکه کار ساخت فایل‌های سایت شما به اتمام رسید، می‌تواند با push کردن در پروژه‌ی صفحه‌ی گیت‌هاب بر روی گیتهاب، سایت خود را آماده کنید.

در مورد صفحه‌ی گیت‌هاب

برای داشتن یک صفحه‌ی گیت‌هاب در سایت Github لازم است یک پروژه با نام <username>.github.io در گیت‌هاب ایجاد نمایید. <username> نام کاربری شما در گیت‌هاب می‌باشد. در نهایت با push کردن فایل‌های ایستای بلاگتان در این پروژه، بلاگ ایستای شما در آدرسی به نام پروژه‌تان ایجاد خواهد شد.

git push -u origin master

اولین پست، ولی آزمایشی

به نام خدا

این یک آزمایش است.

This is only a test.

بعد از اینکه دیدم سایت Koding داون شد، دیدم که مطمئن‌ترین جا برای نوشتن این پست‌ها، همین کامپیوتر خودم هست. بخاطر همین هم Octopress و Jekyll رو کلاً انداختم کنار و رو آوردم به the real thing، یعنی .Net :دی

الان دارم از یک نسخه‌ی تغییر یافته از پروژه‌ی Sandra.Snow استفاده می‌کنم. بعضی تغییرات رو توش اعمال کردم تا کلاً بلاگ برای نمایش فارسی بهتر بشه. البته از کد جاوااسکریپ bidiweb هم استفاده کردم تا متونی که احیاناً بخاطر تغییر زبان به هم بریزن رو درست بکنه. همچنین از کتابخونه‌ی خیلی خوب MathJax هم برای نمایش \(\LaTeX\) استفاده کردم. بعضی وقتا شاید به درد بخورن.

حالا یکم قابلیت‌هایش رو تست بکنیم.

This is a text written in English, and yes it is displayed correctly (not that it wouldn't normally :D)

این هم یه تیکه کد:

using System;

public class test
{
    public static void Main(string[] args)
    {
        Console.WriteLine("Hello World, from Sandra.Snow!");
    }
}

و حالا یکم ریاضی درون یک نوشته‌ی انگلیسی

When \(a \ne 0\), there are two solutions to \(ax^2 + bx + c = 0\) and they are $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}.$$

و همون پاراگراف قبلی به صورت یک پاراگراف فارسی

هرگاه \(a \ne 0\)، دو پاسخ برای معادله‌ی \(ax^2 + bx + c = 0\) داریم که برابر هستند با: $$ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2 a}$$.

و همین دیگه. امیدوارم اونطوری که می‌خوام بتونم بنویسم اینجا و برای خودم و دیگران هم مفید باشه.

تا پستِ بعدی :)