به نام خدا
(Creative Commons Attribution-Share Alike 3.0 Unported license (CC BY-SA 3.0), from Wikimedia Commons)
معرفی
برای بررسی ساختار فرکانسی سیگنالهای متغییر در زمان، از روشی به نام تبدیل فوریهی کوتاه-زمان (STFT) استفاده میشود. با استفاده از این نوع تبدیل فوریه میتوان به اطلاعات فرکانسی و فازی ناحیهای کوتاه از سیگنال پی برد. در حالت پیوسته، این تبدیل از رابطهی زیر به دست میآید:
$$ \text{STFT} \lbrace x(t) \rbrace (\tau ,\omega ) \equiv X ( \tau ,\omega ) = \int _{-\infty }^{\infty} x(t)w(t-\tau )e^{-j \omega t}dt $$
که تابع \( w(t)\) تابع پنجره میباشد.
رابطهی تبدیل فوریهی کوتاه-زمان برای حالت گسسته نیز مشابه میباشد.
$$ \text{STFT} \lbrace x[n] \rbrace (m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty } x[n]w[n-m]e^{-j \omega n} $$
برای تهیهی اسپکتروگرام، سیگنال به بازههایی با طول کمتر از طول سیگنال تقسیم میشود (لزومی ندارد این بازهها مجزا باشند)، برای هر کدام از این بازهها تبدیل فوریه محاسبه میشود، و سپس اندازهی این تبدیل فوریه برای بازههای مختلف در کنار یکدیگر قرار میگیرد تا تصویری دو یا سه بعدی از اسپکتروگرام سیگنال اصلی ایجاد شود.
پیادهسازی
(نمونه کدها، به زبان متلب میباشند)
برای ایجاد نمودار اسپکتروگرام برای یک سیگنال، ابتدا لازم است سیگنال را به تعدادی بازه تقسیم کرده و سپس برای هر بازه، ضرایب فوریه را محاسبه نماییم. در نهایت با جمعآوری همهی این ضرایب به دستآمده، میتوانیم نمودار آبشاری اسپکتروگرام را رسم کنیم.
کد زیر یک پیادهسازی ابتدایی برای این کار است:
function specPlot(x, windlen)
% x: input signal
% windlen: length of the time window inside which fourier coefficients will be calculated, note that since our signal is real, only half of the coefficients are needed
% preallocating magnitude matrix for speedup
numofwinds = floor(length(x)/windlen);
magnitude = zeros(numofwinds, floor(windlen/2));
for i = 0:(numofwinds - 1)
startIdx = i*windlen;
partfft = abs(fft(x((1+startIdx):(startIdx+windlen))))/windlen;
magnitude((i+1),:) = partfft(1:length(partfft)/2);
end
waterfall(1:windlen/2, 0:(length(x)/windlen -1), magnitude);
xlabel('frequency');
ylabel('time');
zlabel('magnitude');
end
حال این توابع را بر روی یک سیگنال نمونه امتحان میکنیم.
سیگنال زیر را که یک سیگنال جیر با رابطهی \( y=sin(1600\pi t^2) \) میباشد در نظر بگیرید. نمودار این سیگنال به صورت زیر است:
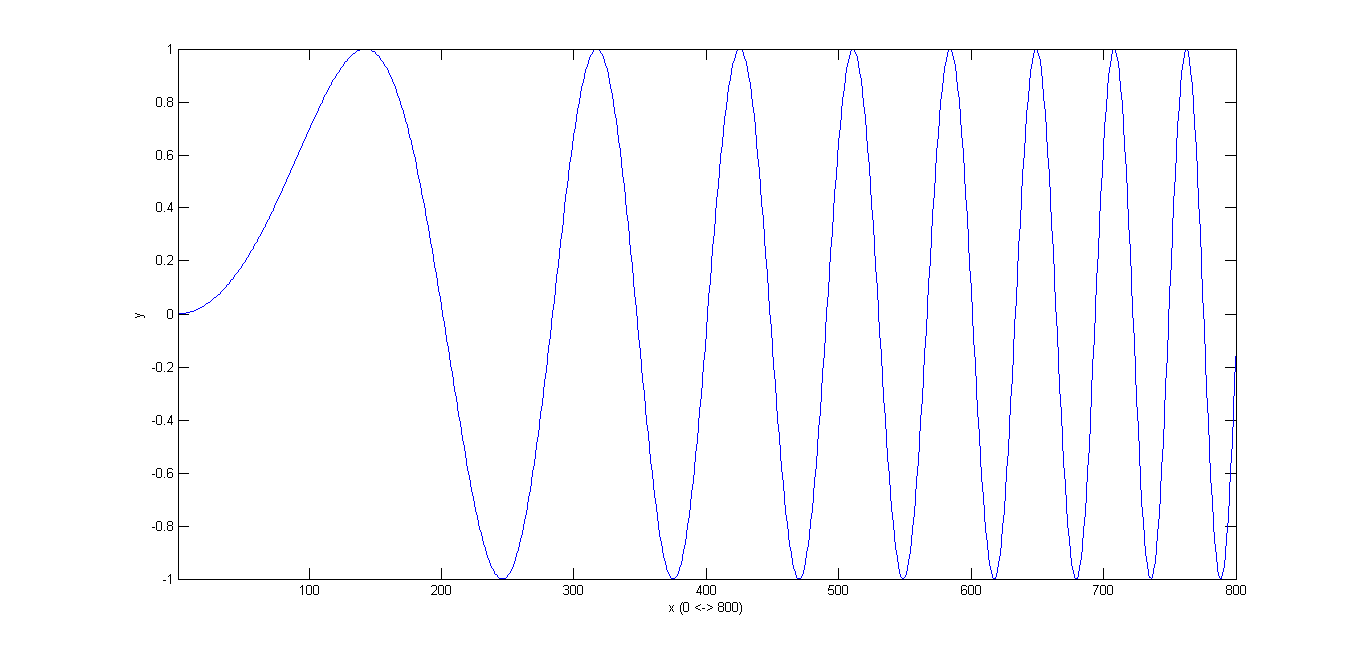
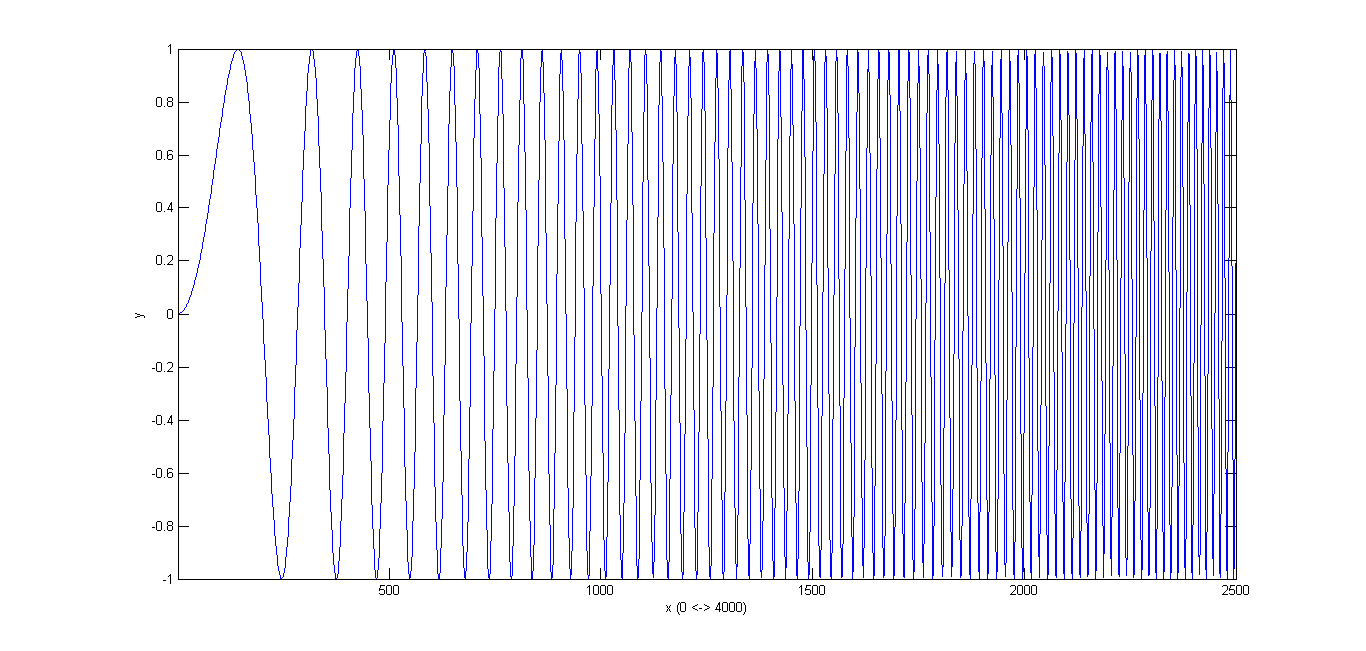
>> t = [0:1/8000:1-1/8000];
>> y = sin(2*pi*800*(t.*t));
>> specPlot(y,800);
با اجرای دستور آخر نمودار زیر ایجاد خواهد شد